About LEOcode
The LEOcode Project
A computational approach to enhancing, measuring, comparing, and matching the papers of Leonardo da Vinci through the detailed encoding and visualization of their internal manufactured patterns including watermarks, chain line intervals, and laid line densities.
The notebooks—codices—of Leonardo da Vinci (1452–1519) have long been the focus of scholarly study spanning many intellectual disciplines. Neglected, separated, dispersed, and recombined after his death, Leonardo’s 4,000+ extant sheets of notes, observations, and drawings present a fascinating puzzle for scholars who strive to recreate their original formats and sequence or simply to better understand the materials and processes behind their fabrication.[1] Concerted efforts have been made to reorder folios and gatherings, propose original collation charts, virtually reintegrate pirated drawings, establish chronology via datable events cited by Leonardo, and cross-reference sheets based upon their subject matter or continuity of discourse.[2]
Tangible traces of material, facture, and function have also been considered when proposing virtual reordering of the codices, the so-called “archaeological” approach. Physical evidence that has been painstakingly recorded by scholars includes page layouts, paleographic oddities, offset writing inks, red chalk transfers, fold lines, water and adhesive stains, sewing holes, remnants of blue cartonnage, indentations from drafting tools, and the determination of original paper formats. Watermark identification, using standard compendia such as Briquet, has promised tantalizing, if problematic, clues for questions of dating and geographic origins.[3] In addition to the endless mining of textual information, interest in materials and techniques remains strong among Leonardo scholars.[4]
In support of this foundational textual and material research, we have computationally “coded” the watermarked papers found in the Codex Arundel (MS 263, British Library) and the Codex Leicester (Gates Collection) through the application of programs that enhance, measure, compare, and match their watermarks and chain line intervals. These procedures, which rely upon visible and more easily and economically generated transmitted light images, have resulted in three benefits for Leonardo scholars:
- substantially improved images of watermarks, chain line intervals, and laid line densities, which are useful for the general characterization of Italian 15th– and 16th-century papers;
- the detection and confirmation of paper moldmates, that is, sheets formed from the exact same papermaking mold, and their probable “twins,” formed from the other alternating mold;
- the accumulation of directly comparable data and animated overlays that indicate potential moldmates and point to new connections.
The existence of moldmates within the Codex Arundel and the Codex Leicester or, by extension, found among other Leonardo papers, raises tantalizing questions vis-à-vis dating and sequence, the artist’s studio practice, individual preferences, and periods of intense activity, as well as patterns of northern Italian paper production and distribution in the 15th and 16th centuries.[5]
What is Computational Coding?
Computational coding is the process whereby a researcher or “coder” examines and transforms a digital image of the watermark and chain lines present in a sheet of handmade paper into a numerical code that can be compared to codes derived from other watermarks and chain lines. While the acquisition of codes may appear complex, user-friendly tools, and tutorials for using them, will facilitate the process. A descriptive overview of the coding process is provided below.
For watermarks, a unique set of points is designated for each watermark type. The ratios of the lengths of the lines connecting these points, together with their angles, generate a numerical code. For chain lines, the code consists of the ratios of the spaces between the chain lines. These codes are ideal for distinguishing minor variations in seemingly identical papers and can be used to confirm that the two papers are (or are not) made from the same mold.
Computational coding is straightforward and uses existing or easily-created digital photographs of the recto and verso and a transmitted light digital photograph of the paper in question.[6] The scale and resolution of the images do not need to be the same. The procedure involves:
- enhancement of the paper’s internal structure (watermarks, chain line intervals, laid line densities) by the virtual removal of surface writing and drawing[7]
- marking and measurement of unique watermark features and chain line intervals and the generation of the codes[8]
- comparison and matching of these codes to identify paper moldmates and their probable twins.[9]
A more detailed technical description of coding is found under The Coding Process.
What are Paper Moldmates and Twins?
In order to appreciate the significance of moldmates and twins for paper studies, it is necessary to understand how they were produced. Moldmates reflect the industrial process of papermaking in Leonardo’s time, that is, one sheet was produced at a time by dipping a rectangular mold into a vat of macerated linen and/or hemp pulp mixed with water. The mold consisted of a porous screen fabricated from fine, densely spaced, horizontal rows of laid wires held into position by widely spaced, vertical chain wires. A removable wooden frame called a deckle surrounded it. When the mold was plunged into the suspended paper pulp and lifted up, the chain and laid wires acted as a sieve. The pulp was retained in thinner and thicker accumulations as the water drained away due to the interference of the laid wires and chain wires. The resulting grid-like configuration can be seen easily when the sheet is placed over a light source. The watermark, formed by stitching a thin wire bent into a simple shape onto the wires of the mold, likewise impeded the rate and quantity of pulp as it drained away, leaving behind a characteristic, translucent impression. After draining, the wet sheet of evenly distributed pulp was transferred from the mold onto a post of freshly formed sheets, each made from one of two alternating molds.
Using a pair of molds was the most efficient means of producing a steady output of individual sheets of paper (see fig. 1, below). The vatman submerged Mold A (circled in red) into the tub, scooped up some paper pulp, and passed the mold to the coucher, who is seen in figure 1 ready to invert a second Mold B (circled in blue) onto the growing post of newly formed paper. The coucher would then slide the emptied Mold B to the vatman, thus creating a continuous cycle.[10] Mold B was watermarked in the same manner as the first.[11] The paper made from this second mold, having the same type of watermark, although not identical, is called a twin. For example, if Mold A had an eagle, Mold B would as well; however, because the watermark forms were hand-fashioned, the eagles would be very similar but not identical.[12] The papers were processed sequentially—stacked and pressed, then air-dried, sized, finished, and packaged. Sequence and output varied roughly according to daily or weekly production runs and the capacity of the drying loft. Papers made from Mold A and its twin, Mold B, were consistently interspersed in individual runs of paper production.[13] It is highly likely that Leonardo’s ream or risma of 500 sheets, or quaderno of 25 sheets, contained moldmates and twins.
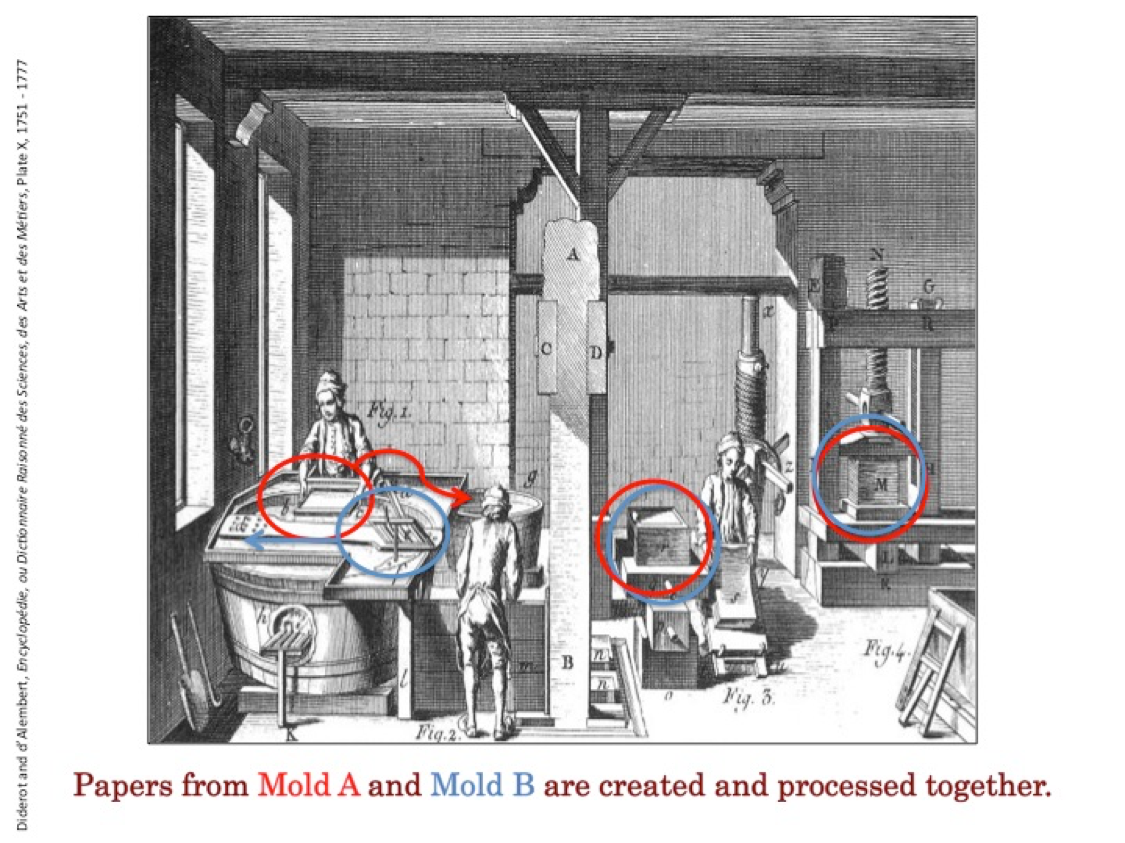
Figure 1: In order to ensure the continuous production of individual sheets of paper, a cycle of two molds was used by the vatman. Papers from the same mold (moldmates) and those from the alternate mold (twins) were processed in tandem throughout each manufacturing phase. The probability of finding moldmates and twins in the final ream of paper is high. (Image: Diderot and d’Alembert, Encyclopédie, ou Dictionnaire Raisonné des Sciences, des Arts et des Métiers, Plate X, 1751-1777).
Being entirely made by hand, every mold was unique, down to the variations in its hand-drawn wires. While at first two molds might appear identical, subtle differences existed in the details of the watermarks, the intervals between chain lines, and the densities of the laid lines (lines per centimeter, see fig. 2, below). The eagle watermark might look the same from one mold to the next; however, its talons could be angled differently or its crown askew. Every sheet of paper formed from a given mold will replicate that mold’s particular physical features.[14]
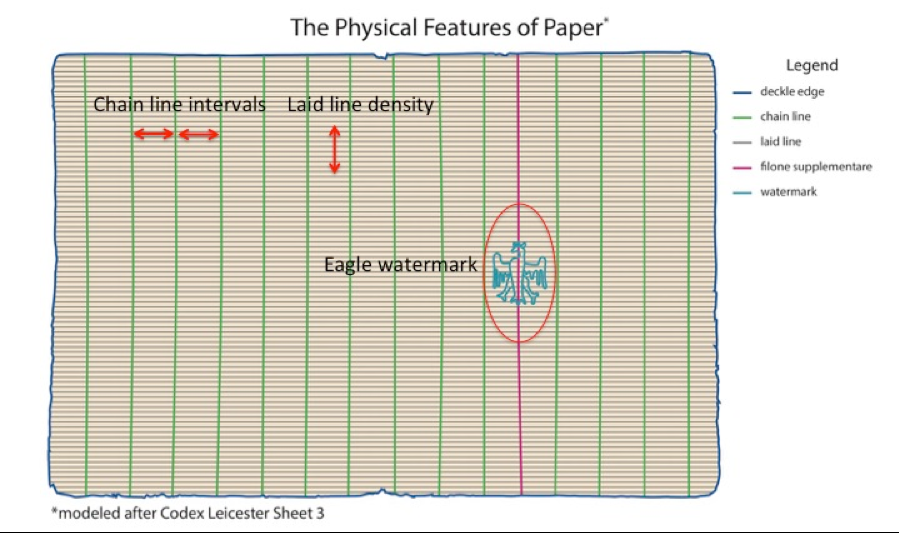
Figure 2: The physical features of a paper reflect the unique characteristics of the papermaking mold used to form it. Moldmates share the subtle variations in watermark details, chain line intervals, and laid line densities. Twins have seemingly identical, but slightly different, physical features. The filone supplementare is a non-supported chain wire characteristic of Tuscan 15th– and 16th-century papermaking molds.[15] (Drawing by A. Slawik)
The Significance of Moldmates
The designation of two sheets of paper as moldmates suggests a common place of origin and a narrow period of production: either from the same production run (days to weeks), or sometime during the lifetime of that one mold (nine months to two years for a popular format).[16] When moldmates and twins (that are themselves moldmates) occur in close sequence, it may be deduced that the papers are from the same ream and, therefore, date from a narrow period of time (days to weeks). Isolated moldmates found out of sequence can be dated to a broader, but still well-defined, period of time (the lifetime of that particular mold).
An accidental accumulation of moldmates in an artist’s workshop or a circumstantial gathering of moldmates by later collectors/custodians is highly unlikely. It is possible that stashes of paper were used at a later point by a workshop. Furthermore, the deliberate selection and arrangement of the moldmates and twins prior to use could not have been an intentional act since their slight physical variations were barely visible to the naked eye and did not impact the appearance or functionality of the paper.
The Codex Arundel and the Codex Leicester as Case Studies
The Codex Leicester and the Codex Arundel were excellent candidates for computational coding for four reasons:
- Digital photographs of the recto and verso[17] and transmitted light digital photographs[18] of their entire sheets were already available and accessible for almost every watermarked folio in both codices.[19]
- Scholars have concluded that portions of the Codex Arundel and the entirety of the Codex Leicester were created between 1505-8 and 1512.[20] Although the proposed dates for individual sections of each codex vary slightly, given the intersection of dates it is reasonable to conjecture that some of the papers in both codices were contemporaneous and, possibly, purchased (or otherwise procured) in batches from a local paper purveyor. This is bolstered by the fact that the two codices share 39 examples of three watermark types: cardinal’s hat, flower, and eagle.
- It has recently been proposed that Leonardo intentionally combined two sets of notes written at different times, which today comprise the Codex Leicester.[21] Moldmates would theoretically be clustered in, but not shared between, each set.
- The papers of the first 14 bi-folios and half sheets of the Codex Arundel were particularly intriguing, due to their eight cardinal’s hat watermarks. Because it has been suggested that Leonardo intentionally compiled this gathering as a discrete “notebook,” it presented a promising source for moldmates and twins.[22]
The Enhancement or “De-noising” of Watermarks and Chain Lines
Because dense writing and drawing on both sides characterize the folios of the Codex Leicester and the Codex Arundel, it is difficult, if not impossible, to record and decipher their watermarks and chain line intervals, much less accurately measure, compare, and match them. For this reason, the moldmates, probable twins, and cross-codex moldmates listed below were derived from enhanced or “de-noised” watermarks and chain lines using a process that makes the paper’s internal structure more visible by virtually removing the obscuring marks on its surface.
The interference of surface marks can be suppressed by computationally processing three images: a visible light digital photograph of the recto surface of the paper; a visible light digital photograph of the verso surface; and a transmitted light digital photograph of the same area.[23] The key idea is to “subtract” optimally weighted versions of the two visible light images from the transmitted light image, leaving behind only the sub-surface features (watermark and chain lines) of the paper. Figure 3 shows the sequence of subtracting two visible light photographs of the recto and the verso of Arundel ff. 3-12 from a transmitted light image of the same sheet. This results in an enhanced—or “de-noised”—image of the cardinal’s hat watermark and of the surrounding chain lines.[24]

Figure 3: Watermarks and chain line intervals are enhanced by subtracting optimally weighted visible images of the recto and verso of Arundel ff. 3-12 (top center and top right) from a transmitted light image of the same area (top left). The resulting image (bottom center) has been “de-noised” of distracting surface marks. (© British Library Board: Arundel 263 ff. 3-12; processed image: William A. Sethares, Ruixue Lian)
Moldmate Matches in the Codex Leicester and the Codex Arundel
A total of 47 selected watermarked sheets from the two codices were computationally enhanced and coded. The results confirmed the presence of 43 paper moldmates and probable twins in the Codex Arundel and the Codex Leicester. Nine papers are cross-codex moldmates, that is, nine sheets formed from the same papermaking mold appear in both codices. This suggests the intriguing possibility that Leonardo was using the same or a closely dated paper source for both manuscripts.
The Codex Leicester
The Codex Leicester, dating from ca. 1505-8 to 1512,[25] consists of 18 disbound reçute or rezzuta[26] format sheets, which were once folded in half.[27] Four watermark types, listed below in order of frequency, are represented:
- cardinal’s hat,
- eagle,
- flower,
- lily.
All the Codex Leicester sheets were de-noised and then the watermarks and chain line intervals measured to acquire their computational codes. As would be expected if different batches of paper from different places at different times were procured and used, strings of moldmates and twins having cardinal’s hat, flower, and eagle watermarks occur regularly throughout the manuscript. These sequences are obvious in the collation chart of the Codex Leicester, which graphically illustrates by color and solid and dashed lines the arrangement of moldmates and their probable twins (see fig. 4).[28] Note that the Codex’s current foliation is depicted.[29], [30] While the traditionally accepted order of the folios cannot be confirmed as having been determined by Leonardo himself, as mentioned above, scholars have recently advanced the idea that Leonardo intentionally combined two sets of notes after they were written at separate times.[31]
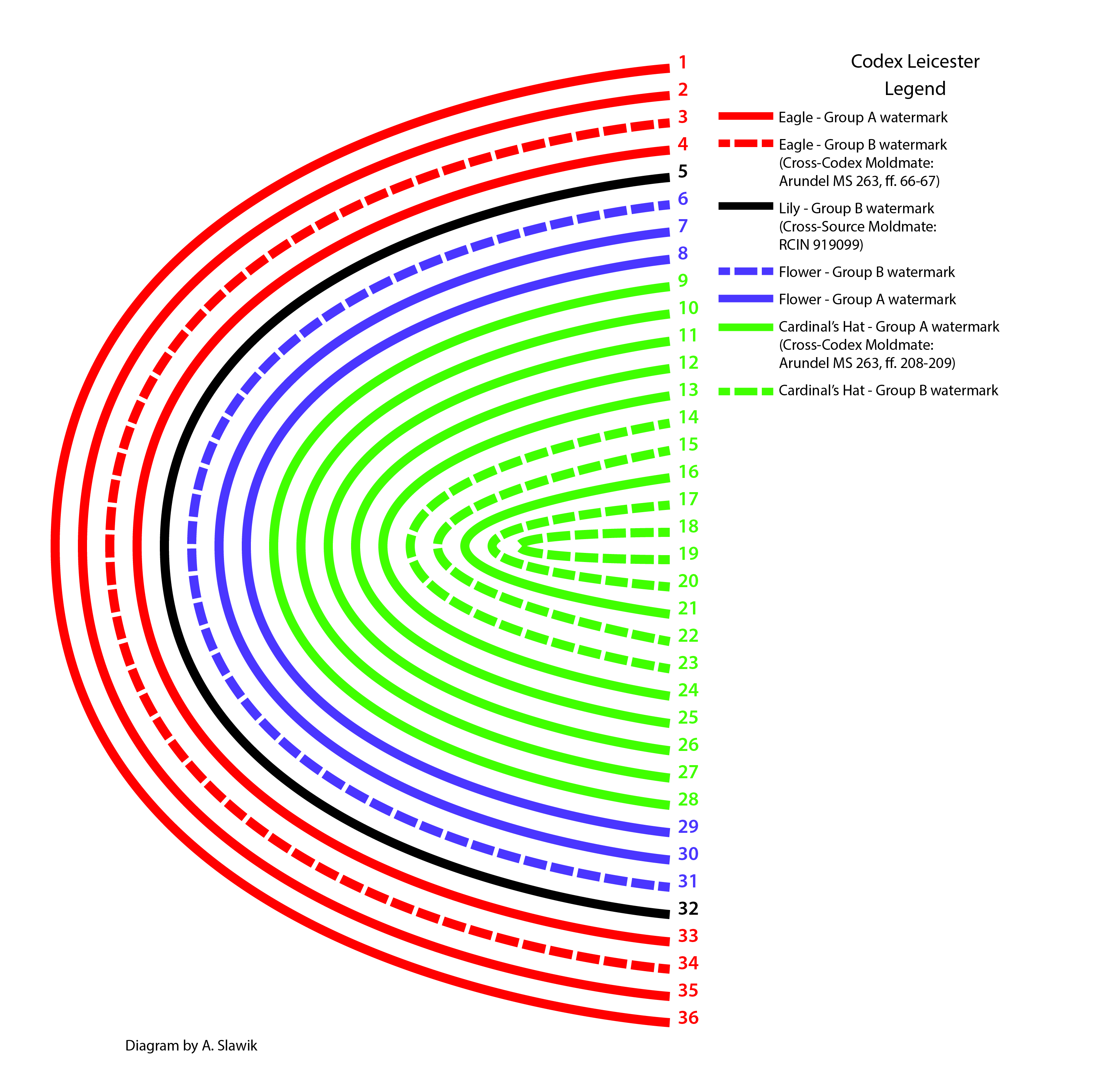
Figure 4: The Codex Leicester with moldmates (solid lines) and probable twins (dashed lines) indicated by color; the current collation of the Codex Leicester is depicted. (Diagram by A. Slawik)
From a codicological point of view, the distribution of moldmates and twins throughout a manuscript can reflect how different paper supplies were obtained and consumed. Based solely on this assumption, the current order of the Codex Leicester seems logical. This does not, however, preclude Leonardo’s deliberate rearrangement of the two sets of writings at the time they were combined. Domenico Laurenza has postulated that the Codex Leicester is made up of inner and outer sets, which “were produced relatively independently at different times, with the ‘outer set’ compiled in a more piecemeal manner, before they were brought together and edited by Leonardo as a 72-page quaderno.”[32] In this scenario, the moldmate status of the sheet in question is still informative, since it can suggest different ordering schemes.
It is also possible that Leonardo selected his papers randomly, saved batches of paper over periods of time, or transported them from location to location. In this scenario, moldmate matches might offer some clues to the artist’s seemingly erratic studio practices. For example, Leicester Sheet 5, having a lily (heraldry) watermark, appears to be an outlier in its current position nestled between eagle and flower moldmates. If contextual evidence confirms that its location is indeed correct, its unique inclusion is still notable, especially if a lily moldmate is eventually located in another collection of Leonardo papers.
The Codex Arundel
The Codex Arundel (MS 263, British Library), composed of 285 disbound bi-folios and half sheets that were assembled by a collector, dates from ca. 1478 to 1518.[33], [34] Therefore, portions of the manuscript overlap in time with the Codex Leicester. Three watermark types, listed below in order of frequency, are shared with the Codex Leicester. A fourth watermark of scissors has been included for coding because of its frequency and moldmate matches found elsewhere in the Codex Arundel:
- cardinal’s hat,
- flower,
- eagle,
- scissors (not shared with the Codex Leicester).
As in the Codex Leicester, computational coding revealed moldmates and probable twins throughout the Codex Arundel (in this case among the cardinal’s hat, flower, and scissors watermark types).
Special attention was paid to the first 30 pages of the Codex Arundel because of their eight recurring cardinal’s hat watermarks, and in light of theories put forward by Bambach and Pedretti/Vecce that the sheets were compiled independently.[35] The codes for these papers were used to create an accurate collation diagram (see fig. 5). The sequences of cardinal’s hat moldmates and probable twins support Bambach and Pedretti/Vecce’s proposal that the gathering is deliberate. No eagle watermarks appear in this section; nine pages do not contain a watermark, which is to be expected in a quarto format constructed from a rezzuta/reçute format sheet.
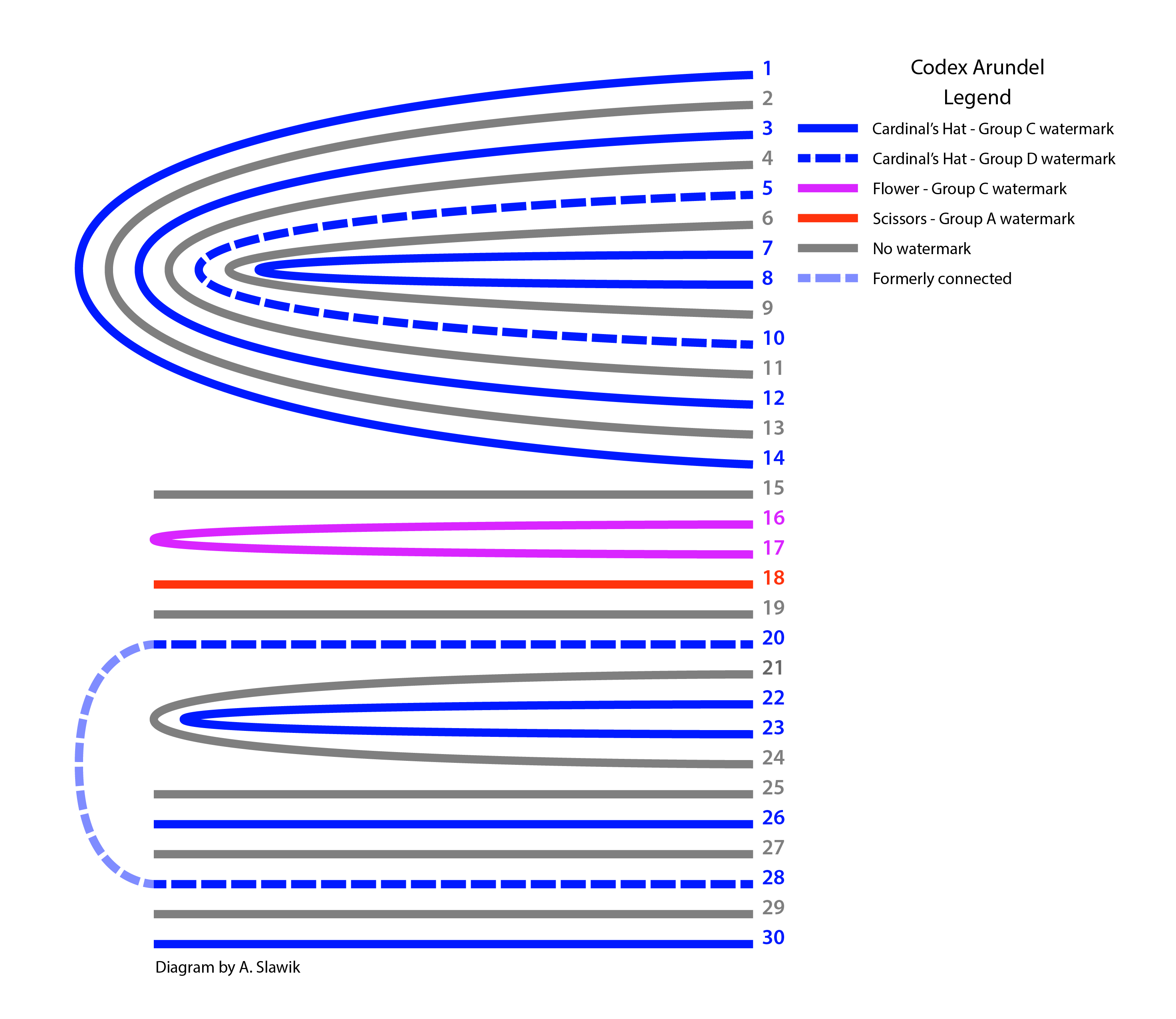
Figure 5: Bi-folios and half sheets 1 through 30 of the Codex Arundel with moldmates (solid lines) and probable twins (dashed lines) indicated by color; the current collation of 1 through 30 is depicted. Note that Arundel ff. 16-17 (flower) and Arundel f. 18 (scissors) have moldmate matches elsewhere in the manuscript. (Diagram by A. Slawik)
Note that the scissors watermark (Arundel f. 18) is a moldmate to four other Arundel bi-folios found elsewhere in the manuscript (ff. 79-93, 147-148, 271-278, and 273-276). Also, Arundel ff. 16-17 (flower) is a moldmate match with two other bi-folios found elsewhere, ff. 173-176 and 282-283. Based solely on physical paper evidence, the insertion of these two sheets into a run of cardinal’s hat moldmates and probable twins, and the fact that they have moldmate matches elsewhere in the manuscript, is notable and suggests a possible past connection between these now separated papers.[36]
Cross-codex Moldmates
The occurrence of nine eagle and cardinal’s hat cross-codex moldmates supports a historical connection between the Codex Arundel and the Codex Leicester. At the very least, the presence of cross-codex moldmates points to affinities of date and place of origin of the sheets and suggests consistent paper sources.
No cross-codex moldmates were found in the first 30 bi-folios and half sheets of the Codex Arundel and the Codex Leicester. While these initial pages share two common watermark types (cardinal’s hat and flower), the two manuscripts contain no physical evidence that they were written using the same batch or closely dated batches of paper. It seems likely that the paper came from the same paper mills, but this is conjecture.
Stepping back from watermarks for a moment, a look at the visible texts and diagrams in the four cross-codex moldmate pages reveals an intriguing inconsistency in their formats and insight into Leonardo’s studio practice. In the case of the cross-codex eagle moldmates, the handwritten passages in Codex Arundel f. 66r and f. 67r are vertically positioned on the left and right halves of the unfolded page, as seen in the right side of figure 6. In the larger Codex Leicester, as seen in the left of figure 6, the text and diagrams likewise appear in a “landscape” format on the left and right halves of unfolded Sheet 3A and 3B. When placed in the proper configuration of their paper formats, Leonardo’s texts and diagrams run perpendicular to each other, as would be expected when writing in a bi-folio versus a quarto format. The arrangements imply that Leonardo either folded the paper beforehand to form a visible centerline or worked with a virtual centerfold in mind.

Figure 6: Leonardo’s writing and diagrams in the eagle cross-codex moldmate folios are perpendicular to each other when the papers are aligned, which properly reflect their bi-folio and quarto formats.
The arrangement of Leonardo’s texts and diagrams are atypical, however, for the cardinal’s hat cross-codex moldmates. In Arundel f. 208r and f. 209r and Leicester Sheet 9A and 9B (taken as a representative of Leicester’s six cardinal’s hat moldmates), the writing is in a vertical form for both (see fig. 7). This may imply that Leonardo did not envision folding the paper in half to form a gathering of notes.
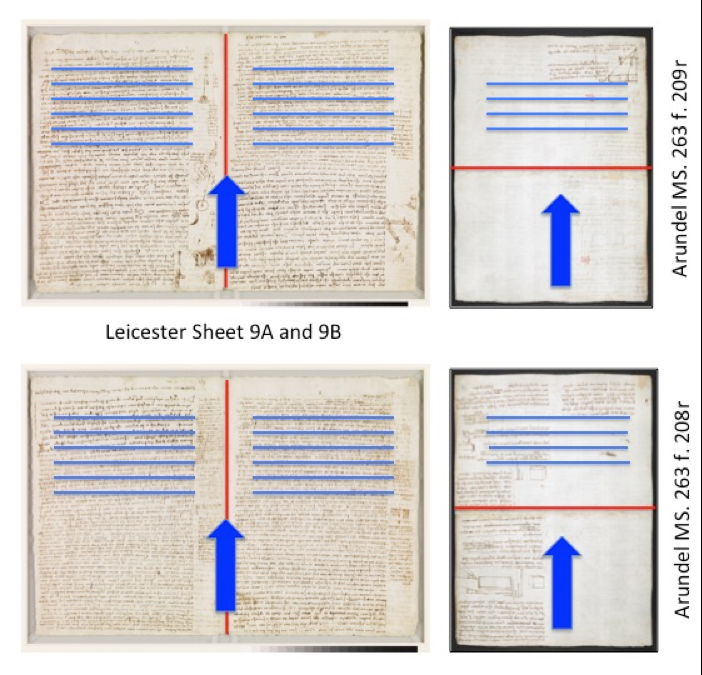
Figure 7: The orientation of the writing that appears on Arundel f. 208r and f. 209r, which shares a cardinal’s hat moldmate with Leicester Sheets 9, 10, 11, 12, 13, and 16, is unusual given its quarto format.
There are other instances of a “portrait” format used in Arundel quarto sheets, for example, Arundel f. 207r and f. 207v, as seen in figure 8.

Figure 8: Other instances of the use of a quarto sheet in a vertical format occur in the Codex Arundel, as seen in the mathematical calculations and text found on Arundel f. 207r and f. 207v.
The Coding Process
Watermarks and chain lines are characteristic internal features of handmade laid papers that have been used to identify sheets formed on the same mold. To help standardize and improve accuracy and confidence in identifying matches, we have developed the quantitative processes described below. These procedures were used to generate the watermark and chain line codes that confirm whether pairs of Leonardo’s papers are or are not moldmates.
Watermark Codes
It is difficult to compare digital images of two similar watermarks having different resolutions, scales, and orientations and verify that they are from the same mold. The approach is to measure distances in pixels between precisely locatable points present in two similar images, and compare ratios of the various distances in one image to the corresponding ratios in the other image.
For example, consider two images of a right triangle with different lengths of vertical and horizontal legs. In the first triangle, the length of one leg is one inch and the length of the other leg is two inches. The first digital image is captured at a resolution of 100 pixels per inch. Thus, the two lengths in this digital image are 100 and 200 pixels. The second digital image is captured at a resolution of 150 pixels per inch, and the two lengths in this second triangle are 150 and 300 pixels. Measured in pixels, the images do not match. Instead, consider the ratio of the measured leg lengths, which effectively cancels the scaling due to the image resolution. For the first image, the ratio of the longer length divided by the shorter length is 200/100=2. For the second image, the ratio is 300/150=2. The triangles thus match each other, having corresponding ratios of 2.
To minimize the human error in marking the distances to be compared, the end points selected must be precisely locatable points in the watermark image or on its nearby chain lines. The left image in figure 9 is the de-noised scissors watermark in Arundel ff. 42-43. The right image in figure 9 marks three precisely locatable points: (i) the lower tip of the left blade, (ii) the upper intersection of the vertical chain line and the watermark, and (iii) the lower tip of the right blade. We are interested in the ratio of the distance from (i) to (ii) and the distance from (ii) to (iii) as an indicator to be compared in the digital image of a similar watermark. If the ratios of the same two lines in two digital watermark images are different, the two watermarks are not moldmates. An animated example of the placement of the red diamonds in a recently discovered set of horn moldmates (Arundel ff. 34-35 and 122-125) can be viewed at https://sethares.engr.wisc.edu/threads/hornWatermarkAnimation.gif
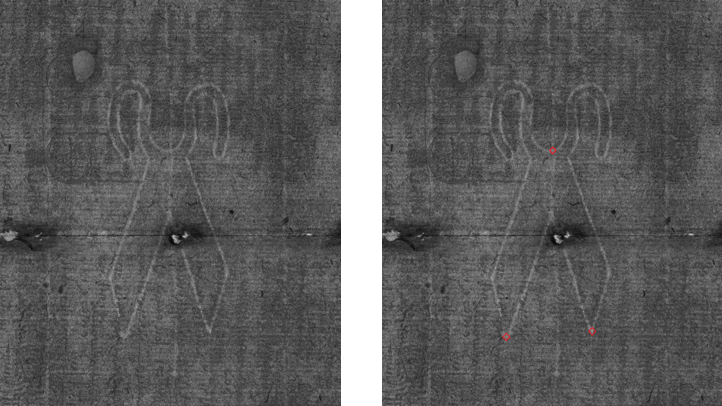
Figure 9: Arundel ff. 42-43, left: de-noised watermark; right: red diamonds marking three points.
To be more confident in declaring two watermarks to be moldmates, we would mark several lines in the two watermarks being compared. The seven lines chosen for a scissors watermark (Arundel ff. 42-43) are shown in figure 10. Note that lines 1 and 2 in figure 10 are, respectively, the lines between points (i) and (ii) and between points (ii) and (iii) on the right in figure 9. For the seven lines in figure 10 the ratios of the lengths of line 6 divided by the lengths of lines 1 through 7 produce the Watermark Code sequence for Arundel ff. 42-43:
0.63, 0.66, 0.96, 1.03, 1.23, 1.00, 1.42

Figure 10: Arundel ff. 42-43: seven lines are used to compose a Watermark Code.
The marked lines at the corresponding locations on the scissors watermarks in Arundel ff. 147-148 and Arundel ff. 273-276 are shown in figure 11. The Watermark Code sequence for Arundel ff. 147-148 is
0.59, 0.60, 1.06, 0.96, 1.11, 1.00, 1.41
For Arundel ff. 273-276, the Watermark Code sequence is
0.61, 0.61, 1.09, 0.98, 1.11, 1.00, 1.42
Given the inaccuracies in marking the chosen points in the images, we chose to declare two Watermark Code sequences the same only if all entries were within 0.1 of their corresponding value in the other image. Furthermore, the range of values across a group of moldmates should be 0.1 or less for all entries. The fifth value in the sequence for Arundel ff. 42-43 fails this requirement in comparison to the fifth values in the sequences for Arundel ff. 147-148 and Arundel ff. 273-276. However, the Watermark Code sequences for Arundel ff. 147-148 and Arundel ff. 273-276 do satisfy the matching criterion. Therefore, Arundel ff. 147-148 and Arundel ff. 273-276 are moldmates, while Arundel ff. 42-43 is from a different mold.

Figure 11: Additional scissors watermarks from the Codex Arundel, left: Arundel ff. 147-148; right: Arundel ff. 273-276.
In order to be even more confident, we also derived Watermark Angle sequences by recording the angles between pairs of the seven marked lines that share an end point. In figure 11, the line pairs forming angles are 1-2, 3-4, 4-5, 5-6, and 6-7. All angles in a Watermark Angle sequence must be within three degrees of the corresponding angle for two watermarks to be declared moldmates. The results for the Watermark Angle sequences for Arundel ff. 42-43, Arundel ff. 147-148, and Arundel ff. 273-276 are the same as the moldmate designations from the Watermark Codes. The difference is quite visible in figure 11. The angle formed by lines 3 and 4 is less than 90 degrees in Arundel ff. 42-43 in figure 10 while in figure 11 showing Arundel ff. 147-148 and Arundel ff. 273-276 it is greater than 90 degrees.
In this example, a visible watermark feature distinguishes Arundel ff. 42-43 from the moldmate pair shown in figure 11, Arundel ff. 147-148 and Arundel ff. 273-276. The gap in the left handle at the top of the scissors in Arundel ff. 42-43 is visibly narrower than the similar gaps in Arundel ff. 147-148 and Arundel ff. 273-276. This provides confirmation of the validity of our procedure.
Chain Line Codes
Chain lines in the papers under investigation are spaced approximately one inch apart. Because papermaking molds are handmade, the sequence of chain wire intervals varies modestly across one mold and also from mold to mold. As with digital images of watermarks, digital images of sheets of paper revealing the chain lines are frequently collected at different resolutions.
Furthermore, the images may not have the chain lines oriented precisely vertically. Therefore, an accurately measured interval will depend on the angle of the parallel chain lines relative to the horizontal marking line. If the chain lines are perfectly vertical, and therefore have a 90-degree angle with the horizontal marking line, the distance will be smaller than for any other relative angle between the chain lines and the horizontal marked stripe. This is another issue that is resolved by using ratios.
A final concern that needs to be addressed is that the chain lines may not be perfectly straight or precisely parallel to each other. Consequently, the chain line space sequence for a horizontal line drawn across a sheet of paper can be slightly different if taken at different vertical coordinates. To mitigate this effect, the horizontal marking line crossing the approximately vertical chain lines should be placed at the same location in each of the sheets being compared. For example, consider the three horizontal stripes drawn across the bottom tips of the scissors in Arundel ff. 42-43, Arundel ff. 147-148, and Arundel ff. 273-276 as illustrated in figure 12.

Figure 12: Marked stripes, top: Arundel ff. 42-43; middle: Arundel ff. 147-148; bottom: Arundel ff. 273-276.
The Chain Line Code sequence in these three images with the six spaces numbered left to right are the five ratios of the space widths 1/2, 2/3, 3/4, 4/5, and 5/6. The resulting Chain Line Codes are
Arundel ff. 42-43 0.96, 1.16, 1.18, 0.76, 0.97
Arundel ff. 147-148 1.02, 1.20, 1.00, 0.83, 0.97
Arundel ff. 273-276 1.02, 1.21, 0.99, 0.82, 0.97
The bold number is the ratio spanning the watermark. This ratio must be aligned for a proper comparison of a pair of watermarks. The tolerance allowed for moldmate declaration is the same as for the Watermark Codes, i.e., within a range of 0.1 in every entry. By this criterion, we reached the same match assessment as with the Watermark Codes. Arundel ff. 147-148 and Arundel ff. 273-276 are moldmates, while Arundel ff. 42-43 is from a different mold.
Laid Line Density Maps – Work in Progress!
Like the intervals between vertical chain wires, the distribution of closely spaced horizontal laid wires across the porous screen of a papermaking mold fluctuates in a pattern unique to that mold.[37] Measured in lines (or wires) per inch/centimeter, laid line density patterns can be “mapped” according to various colors: in figures 14, 15, and 16, regions of low density are colored blue and regions of higher density are colored red.[38] The patterns formed by laid line density maps can add to the information derived from watermark details and chain line intervals. Like Chain Line Codes, laid line density maps can also be used in the case of fragmentary or missing watermarks.
Eight folios in the Codex Arundel have watermarks depicting scissors. Two (Arundel f. 18 and ff. 79-93) are half sheets and contain only the lower portion of the blades of the scissors, making the application of Watermark Codes impossible. While Chain Line Codes (fig. 13) confirm that they are moldmates, the laid line density maps (fig. 14) for these two sheets are remarkably similar. Furthermore, the maps of these half sheets correspond with the lower portion of the laid line density maps (fig. 15) for Arundel ff. 147-148, 271-278, and 273-276, that are already confirmed as moldmates from their chain line intervals (fig. 13). The stark difference between laid line density maps of papers made from two different molds can be seen in figure 16, which depicts Arundel ff. 42-43, the outlier seen in the orange dotted line in figure 13.
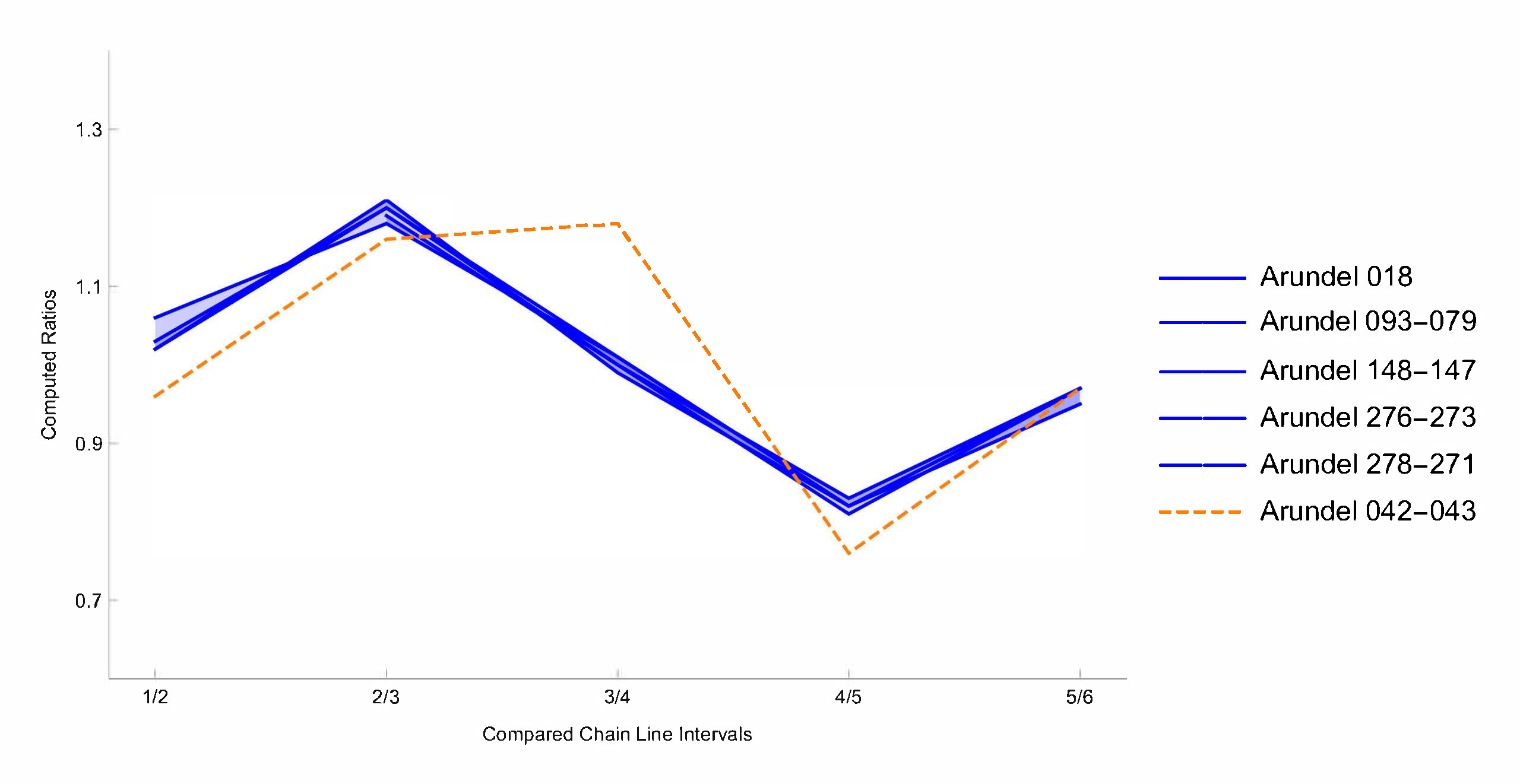
Figure 13: The chain line visualization of the scissors watermarks in the Codex Arundel is consistent with classification of the five blue lines as moldmates, while the one (Arundel ff. 42-43) in dotted orange is an outlier. (Processed marked images and extracted ratio graphs: William A. Sethares, Ruixue Lian, C. Richard Johnson, Jr.)
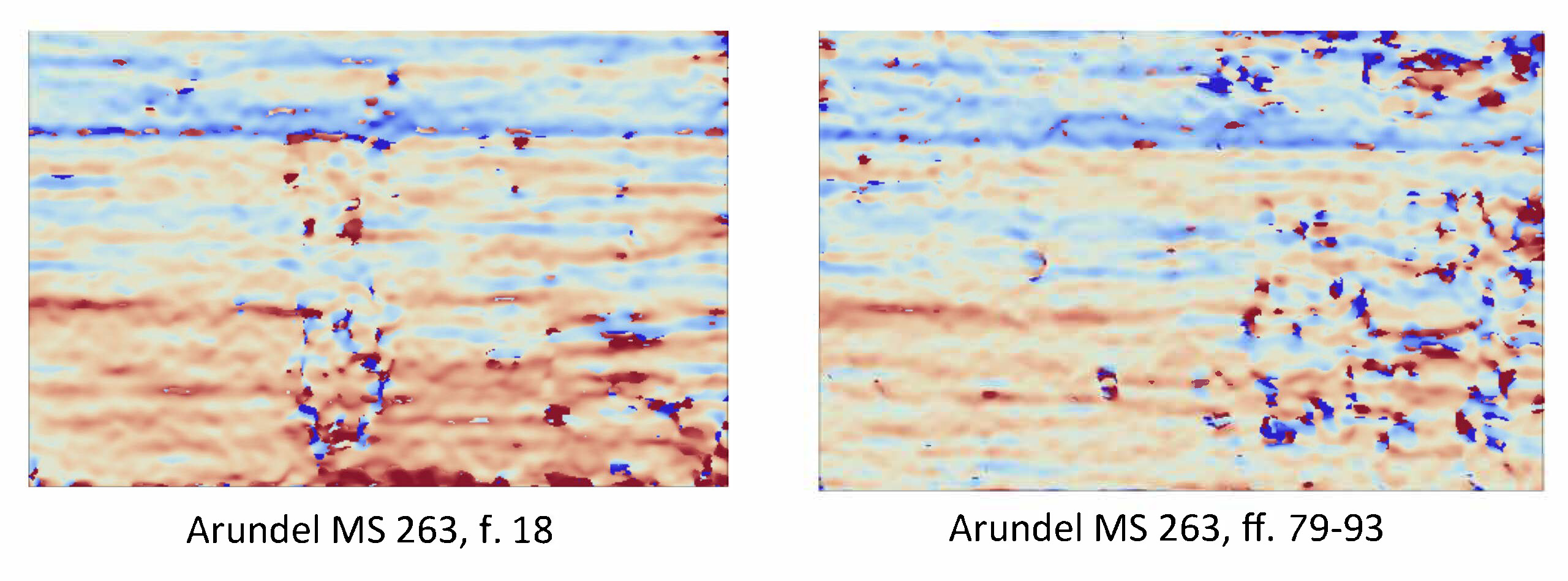
Figure 14: Laid line density maps of two half sheets (Arundel f. 18 and ff. 79-93) having only fragmentary scissors watermarks show similar distribution patterns that support their designation as moldmates in the chain line visualization (fig. 13). (Processed laid line density maps: William A. Sethares)
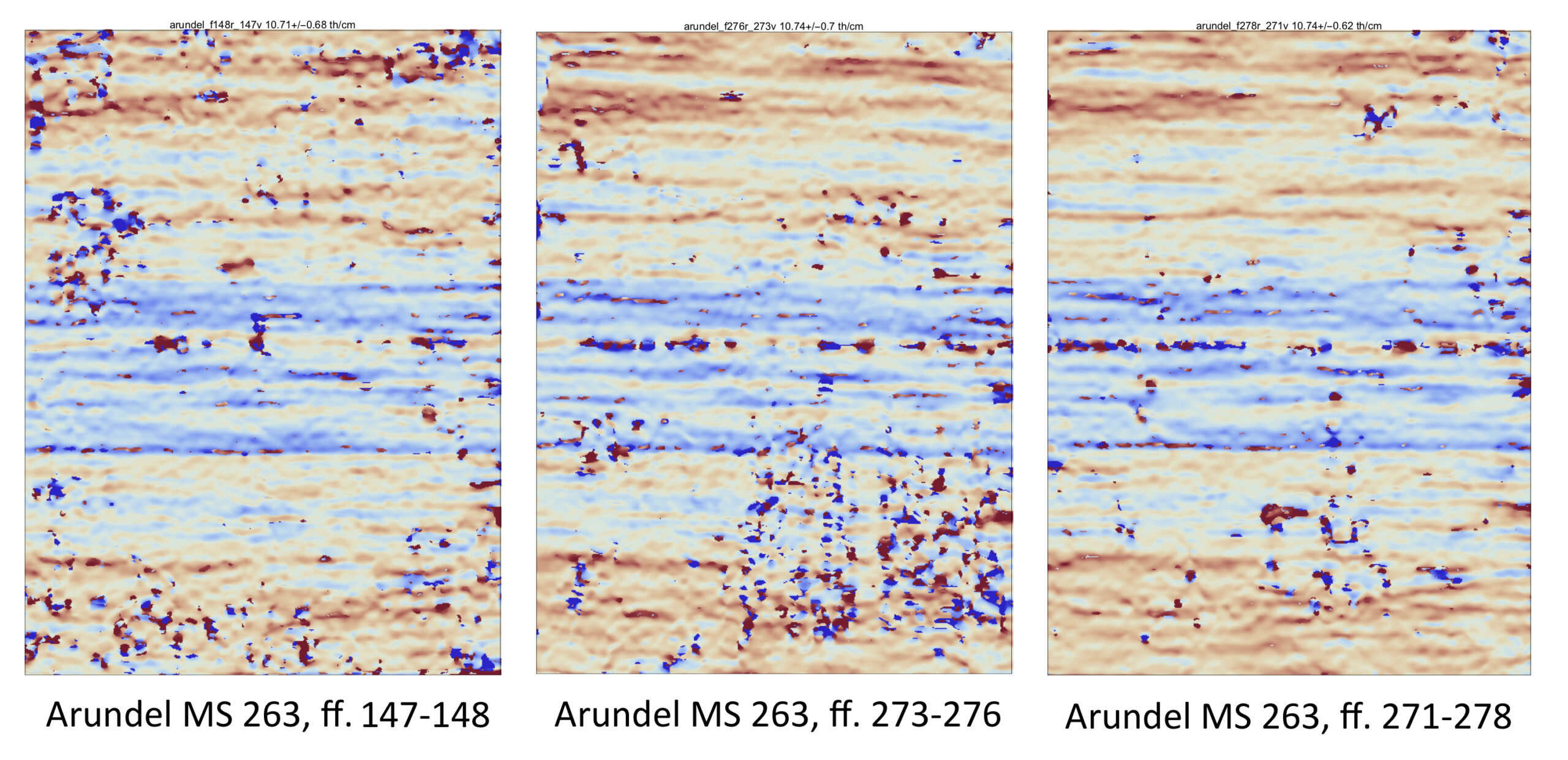
Figure 15: Laid line density maps of the two half sheets seen in figure 14 correspond closely to the lower halves of the laid line density maps for Arundel ff. 147-148, 273-276, and 271-278 and support the designation of all five papers as moldmates in the chain line visualization (fig. 13). (Processed laid line density maps: William A. Sethares)

Figure 16: A comparison of laid line density maps for Arundel ff. 147-148 and the outlier Arundel ff. 42-43, seen in figure 13, show significantly different distribution patterns. (Processed laid line density maps: William A. Sethares)
Computational Coding as a Tool for Paper Studies
In keeping with the current archaeological approach in the investigation of Leonardo’s manuscripts, computational coding measures, compares, and matches specific physical properties of his papers.[39] While the results can illuminate fascinating patterns of moldmates and probable twins that point to chronology and original collation, coding cannot substitute for extensive paleographic observations, conceptual analysis of Leonardo’s writings, or an in-depth knowledge of the history of their creation, agglomeration, and dispersal. Watermarks, in and of themselves, as Bambach points out, “do not provide absolute data, and must be very carefully contextualized with historical and stylistic evidence.”[40] Intended to be of service to scholars, the moldmate matches found in this working compendium support the historical connection between the two codices, the segmented, but intentionally combined, contents of the Codex Leicester, and the deliberate compilation of the first 30 bi-folios and half sheets in the Codex Arundel. The identification of moldmate sequences located elsewhere in the Codex Arundel raises intriguing questions of collation since these papers are related by virtue of their date and place of manufacture.
The results of the case studies provided by the Codex Leicester and the Codex Arundel promote the application of computational coding to collections of contemporary documents or other closely affiliated sources. Potentially fruitful sources might include the drawing papers of Albrecht Dürer (1471-1528), possibly shared papers of Rembrandt (1606-1669) and Ferdinand Bol (1616-1680), large scale multi-sheet maps and prints, music scores, and disbound, reordered, or scattered manuscripts and sketchbooks, such as those of Jan van Goyen (1596-1656).[41]
Selected portions of the text above appear in The Quarterly, British Association of Paper Historians, No. 119, July 2021. 1-18.
Notes:
[1] For a description of the dispersal of Leonardo’s manuscripts, see Juliana Barone, “Introduction,” in Leonardo in Britain: Collections and Historical Reception: Proceedings of the International Conference, London, 25-27 May 2016, ed. Susanna Avery-Quash and Juliana Barone (Firenze: Leo S. Olschki Editore, 2019), xxv-xxvi. https://arthistoriography.files.wordpress.com/2019/08/leonardo-in-britain-intn.pdf
[2] Extensive studies of Leonardo’s notebooks have been conducted principally by Gerolamo Calvi, I manoscritti di Leonardo da Vinci dal punto di vista cronologico, storico e biografico, Bologna: Zanichelli, 1925 (reprint: Augusto Marinoni (ed.): Busto Arsizio: Bramante, 1982); Carlo Pedretti, A Chronology of Leonardo da Vinci’s Architectural Studies after 1500 (Geneva: E. Droz, 1962); The Literary Works of Leonardo da Vinci, 3rd ed., Jean Paul Richter, ed. (London and New York: Phaidon, 1970); The Literary Works of Leonardo da Vinci, ed. Jean Paul Richter with commentary by Carlo Pedretti (Berkeley and Los Angeles: University of California Press, 1977); Carlo Pedretti, The Codex Atlanticus of Leonardo da Vinci: A Catalogue of Its Newly Restored Sheets, 2 vols. (New York: Johnson, 1978); Carlo Pedretti in The Codex Hammer of Leonardo da Vinci, ed. C. Pedretti (Florence: Giunti, 1987); Bambach, Leonardo da Vinci Rediscovered, 4 vols. (New Haven and London: Yale University Press, 2019); Domenico Laurenza and Martin Kemp, eds., Leonardo da Vinci’s Codex Leicester: A New Edition, 4 vols. (Oxford and New York: Oxford University Press, 2019-2020); Juliana Barone, ed., Leonardo da Vinci: A Mind in Motion, exh. cat. (London: The British Library, 2019); Paolo Galluzzi, Water as Microscope of Nature: Leonardo da Vinci’s Codex Leicester (Florence: Giunti, 2018).
[3] Briquet, Les Filigranes: Dictionnaire historique des marques du papier dès leur apparition vers jusqu’en 1600, 4 volumes (Geneva: A. Jullien, 1907); Aurelio and Augusto Zonghi, Zonghi’s Watermarks: The Watermarks Collected by A. & A. Zonghi as Traced from the Original Papers by C. Canavari, Monumenta chartæ papyraceæ historiam illustranti, vol. 3. (Hilversum, Holland: The Paper Publications Society, 1953). Thanks to the Bernstein Consortium and the Fondazione Fedrigoni Fabriano, these historic tracings made by hand are now available online: The Memory of Paper (website), Bernstein Consortium, updated November, 27, 2019, http://www.memoryofpaper.eu; Corpus Chartarum Fabriano (website), Fondazione Fedrigoni Fabriano, accessed February 6, 2020, http://www.fondazionefedrigoni.it/. Other watermark collections, such as the one compiled by Gerhard Piccard, can be accessed via the Watermark Information System hosted by the German Research Foundation, Wasserzeichen-Informationssystem, accessed February 6, 2020, https://www.wasserzeichen-online.de/wzis/projekt/index.php.
The authors recognize the accumulation and cross-referencing of Leonardo’s watermarks by Martin Clayton (The Royal Collection), the detailed documentation of watermarks found in the Codex Arundel by Carlo Pedretti and Carlo Vecce (Il Codice Arundel 263 nella British Library), and the ambitious project to transcribe via line drawings the watermarks found in the Codex Atlanticus (Biblioteca Pinacoteca Ambrosiana) by Claudio Calì under the leadership of Pietro C. Marani and presented at Decoding Leonardo’s Codices, hosted by the Kunsthistorisches Institut and the Museo Galileo, Florence, November 2019. A recording of the entire symposium is found at https://vimeo.com/showcase/6528343 and essays from the proceedings were published in Paolo Galluzzi and Alessandro Nova, eds., Decoding Leonardo’s Codices: Compilation, Dispersal, and Reproduction Technologies (Venice: Marsilio, 2019).
[4] Most recently, Musée du Louvre, Léonard de Vinci: Dessins et manuscrits, exh. cat. (Paris: Musée du Louvre, 2003); Michel Menu, ed., Leonardo da Vinci’s Technical Practice: Paintings, Drawings and Influence (Paris: Hermann, 2014); Martin Clayton, Leonardo da Vinci: A Life in Drawing (London: Royal Collection Trust, 2018); Alan Donnithorne, Leonardo da Vinci: A Closer Look. Exploring the Beauty and Complexity of Leonardo’s Drawings through a Study of his Materials and Methods (London: Royal Collection Trust, 2019); Juliana Barone 2019; Bambach 2019; Benedetta Spadaccini, ed., Leonardo da Vinci e il suo lascito: gli artisti e le tecniche, exh. cat. (Milan, Pinacoteca Ambrosiana, 2019). There is a section on “New Physical Evidence” in Laurenza and Kemp 2019-2020, vol. 3, 319-322.
[5] Portions of the Codex Arundel and the entirety of the Codex Leicester were probably created during the same narrow period of time, with proposed dates ranging from 1505 to 1518. (See note 20). This chronology was first advanced by Calvi and later strengthened by Pedretti (1987, xix), who observes Leonardo’s references to Florence and Tuscany in terms of physical geology and available resources, such as suitable clay for pottery. See also Bambach 2019, vol. 3, 273-274.
[6] Requirements for suitable digital images are described under Imaging Guidelines.
[7] The software required to enhance watermarks will be part of a package, produced with the help of the Getty Foundation, to be distributed under an open-source license. A more detailed description of the process may be found in William A. Sethares, Margaret Holben Ellis, and C. Richard Johnson, Jr., “Computational Watermark Enhancement in Leonardo’s Codex Leicester,” Journal of the American Institute for Conservation 59, no. 2 (March 2020): 87-96, https://doi.org/10.1080/01971360.2019.1703483.
[8] The necessary programs watermarkMarker, chainLineMarker, watermarkPointMarker, watermarkLibrarySearch, and watermarkLibraryBuilder are available to download as free and open-source software.
[9] Tutorials are being developed that will allow institutions to code and identify moldmate matches within groups of related papers in their collections.
[10] The authors are grateful to Neil Harris for his clarification of the coucher’s actions.
[11] The watermarks on the alternating pair of molds were placed on the center right half and the center left half sides respectively, usually one chain line from the center, as described in Sylvia Rodgers Albro, Fabriano: City of Medieval and Renaissance Papermaking (New Castle and Washington, D.C.: Oak Knoll Press and The Library of Congress, 2016), 69. Their original location can be determined by their coordinates as measured from the wire side of the sheet. It was not possible to differentiate the wire side from the felt side from images of the Codex Leicester and the Codex Arundel; however, this determination does not affect moldmate matching.
[12] Furthermore, the wires forming the watermark were bent around a jig or channel, so twin watermarks usually share the exact outside dimensions. From the early 14th century onwards, twin watermarks were secured on the opposite halves of their respective molds. Computational coding is not influenced by this factor, but it is useful when examining the actual sheets. We are grateful to Neil Harris for bringing this to our attention.
[13] Allan Stevenson, “Watermarks are Twins,” Studies in Bibliography, vol. 4 (1951-52): 87-90; Paul Needham, “The Study of Paper from an Archival Point of View,” IPH Yearbook 7: Papers of the 19th International Congress of Paper Historians, Durham and Hertford, 4-10 September 1988 (1988): 122-135.
[14] Substantial progress has recently been made in producing laid line density maps that can be used to match papers lacking watermarks. See Sara F. Gorske, C. Richard Johnson, Jr., William A. Sethares, Margaret Holben Ellis, Paul Messier, “Moldmate identification in pre-19th-century European paper using quantitative analysis of watermarks, chain line intervals, and laid line density,” International Journal for Digital Art History, March 2021. https://dahj.org/article/moldmate-identification-in-pre-19th-century-european-paper-using-quantitative-analysis-of-watermarks-chain-line-intervals-and-laid-line-density.
[15] The chain line supporting most of the watermarks found in the Codex Arundel and the Codex Leicester is, in fact, a filone supplementare. There are no shadows surrounding a filone supplementare because there is no wooden rib below it. The prevalence of the filone supplementare supports a Florentine origin for the Codex Leicester and the first thirty pages of the Codex Arundel. Watermarks located between chain lines, such as Flower Group C, do not have a filone supplementare.
[16] The lifetime of a papermaking mold is dependent upon its dimensions, with popular sizes being more short-lived since they were used the most. Based on estimates found in the literature, Neil Harris has suggested one to two years, with the caveat that older molds continued to be used as they were phased out (personal communications, March 5, 2020 and January 6, 2021; also Harris, Paper and Watermarks, 46, 76-77). Additionally, molds could be sold as material assets and change their place of origin. That is why the position of one watermarked sheet relative to other identical watermarked sheets within a manuscript is critical.
[17] Digitized images of all 285 folios are freely available at http://www.bl.uk/manuscripts/FullDisplay.aspx?ref=Arundel_MS_263.
[18] The authors are grateful to Dr. Andrea Clarke, Curator, British Library, and Fred Schroeder, Curator of the Codex Leicester, for generously sharing these transmitted light images. In addition to viewing differences in paper translucency via transmitted light, there are other means of detecting and recording the inner structural features of paper with varying degrees of accuracy; see Margaret Holben Ellis and C. Richard Johnson Jr., “Computational Connoisseurship: Enhanced Examination Using Automated Image Analysis,” Visual Resources 35, no. 1-2 (2019): 125-140. Harris has written extensively about the history of reproducing watermarks and the advantages and disadvantages of each method, in Paper and Watermarks as Bibliographical Evidence, 2017. Methods dependent upon differences in paper density include tracing by hand over a light source; exposure to a photo-sensitive proofing paper such as DYLUX, largely discontinued; β-radiography; low energy χ-radiography; and reflected infrared (IR) and various multispectral imaging approaches (Harris, Paper and Watermarks, 54-57). Methods dependent upon differences in paper topography include rubbing the wire or mold side of the paper with a soft pencil, largely discontinued; and Reflectance Transformation Imaging (RTI), K. Heumiller, S. Choi, J. Stenger, and C. Graham, “Post Processing of Reflectance Transform Imaging for Isolation of Surface Impressions,” Archiving 2016: Final Program and Proceedings (Springfield, VA: Society for Imaging Science and Technology, 2016), 15–20.
[19] Digital photographs of 13 out of 87 full or partial watermarks found in the Codex Arundel were not available at the time of this writing.
[20] The most recent dating proposal of 1505-8 to no later than 1512 is found in Laurenza and Kemp 2019-2020, vol. 2, 38-39.
[21] The new proposal of the two sets has been presented in Laurenza and Kemp 2019-2020, vol. 2, 15-16 and Domenico Laurenza, “The Compilation of the Codex Leicester: An Insight into Leonardo’s Research Style,” in Paolo Galluzzi and Alessandro Nova, eds., Decoding Leonardo’s Codices: Compilation, Dispersal, and Reproduction Technologies (Venice: Marsilio, 2019).
[22] Pedretti and Vecce observed repeating cardinal’s hat watermarks in the first 30 pages of the Codex (Pedretti and Vecce, Il Codice Arundel 263 nella British Library, vol. 4, 53). Bambach observed that the first 28 leaves of the Codex Arundel appear to have been originally a “unitary notebook or nestled loose sheets” and that Arundel 1v-14r once made up its “exterior cover or guard” (Bambach, Leonardo da Vinci Rediscovered, vol. 4, 327, n. 50). Both references make note of a recurring cardinal’s hat watermark; if Leonardo was using one batch of paper, this phenomenon would not be surprising.
[23] In the past, only the watermark and its adjacent chain lines were imaged. Full sheet images are preferable since they allow for the analysis of the chain line intervals and laid line densities, which can be used to confirm fragmentary watermarks.
[24] William A. Sethares, Margaret Holben Ellis, and C. Richard Johnson, Jr., “Computational Watermark Enhancement in Leonardo’s Codex Leicester.”
[25] Laurenza and Kemp 2019/2020, vol. 2, 38-39.
[26] Also spelled rezuta. Brian Richardson, Printing, Writers and Readers in Renaissance Italy (Cambridge and New York: Cambridge University Press, 1999), 11; Harris, Paper and Watermarks, 96. On the late 14th-century “Bologna stone,” a publicly displayed slab incised with standard paper sizes and their names, the format is spelled reçute (Museo Civico Medievale, Bologna, inv. 1637).
[27] The dimensions of the opened folios are approximately 300 x 400 mm (11 13/16” x 17 23/32”). Nicholas Pickwoad has observed that since the Codex Leicester is folded in folio format, with uncut edges, it is to be expected that there will be deckle edges evident on all three outer edges of each leaf; this is mostly the case, except for the first six sheets which all have edges which have been trimmed to a greater or lesser extent. This would appear to have been done in response to damage along the relevant areas of edge, with sheets 1 and 2 being trimmed on all three outer edges (Pickwoad, unpublished report).
Each open sheet is divided into four folios – two on the recto and two on the verso. Since many scholars refer to individual folios in the Codex Leicester rather than entire sheets, a concordance has been included which designates each folio according to traditional codicological syntax. A second concordance has been included that cross-references the ordering system devised by Carlo Pedretti in The Codex Hammer of Leonardo da Vinci, ed. C. Pedretti (Florence: Giunti, 1987). Readers with an interest in 15th-century paper are urged to investigate a tool for manuscript scholars and art historians that can be used to determine original paper formats: The Needham Calculator 1.0 (website), The Schoenberg Institute for Manuscript Studies, University of Pennsylvania Libraries, accessed July 15, 2021: http://needhamcalculator.net.
A note on the terms bi-folio, folio, and sheet:
Bi-folio: one sheet of paper in a codex, folded in half along the spine. Plural: bi-folios.
Folio: a leaf from a codex, typically one half of a bi-folio. Plural: folios. Folios are numbered according to the sequence in which they appear in the codex. Each folio is typically still attached along the spine-fold to the other half of the bi-folio. For example, Arundel Folio 1 is attached along the spine-fold to Arundel Folio 14 (see fig. 5). Together, this folded piece of paper is referred to as Arundel Bi-folio 1v-14r, or simply Arundel 1v-14r. However, some folios in the Codex Arundel are not attached to any others. These folios are referred to as half sheets. For example, Arundel Half Sheet 15, or Arundel 15; Arundel Folio 15 is also accurate.
Sheet: Another word for the paper that makes up a bi-folio. In the Codex Leicester, each sheet is uncut, with four deckle edges remaining from the rezzuta format paper mold. Today the Codex Leicester consists of 18 now-opened bi-folios with each sheet simply numbered 1 – 18 and lettered A/B to indicate recto/verso. This system is contrary to a traditional codicological numbering system whereby each opened sheet is divided into four folios—two on the recto and two on the verso of the horizontally-oriented paper. Since scholars often refer to individual folios in the Codex Leicester rather than entire sheets, two concordances have been included which designate each folio according to its traditional codicological syntax. Each sheet is still intact along the spine-fold. For example, folios 1 and 36 are attached; folios 2 and 35 are attached (see fig. 4). Therefore, the authors use the terms Leicester Sheet 1 and Leicester Sheet 2, instead of Leicester Bi-folio 1-36 and Leicester Bi-folio 2-35, although either term is technically accurate. The uncomplicated collation of the Codex Leicester allows for this simplified terminology.
[28] Because a lily (heraldry) watermark was not present in the Codex Arundel for comparison and matching, Leicester Sheet 5 was enhanced, but not coded.
[29] Victoria Blyth-Hill, “Conservation Treatment of a Leonardo da Vinci Manuscript,” Preprints of Papers Presented at the Tenth Annual Meeting, Milwaukee, Wisconsin, 26-30 May 1982 (Washington, D.C.: American Institute for Conservation of Historic and Artistic Works), 113-123.
[30] The recorded foliation can be seen in plate 10.143, Bambach, Leonardo da Vinci Rediscovered, vol. 3, 268 and Blyth-Hill, “Conservation Treatment of a Leonardo da Vinci Manuscript,” 113, as recorded by Gerolamo Calvi, Il codice di Leonardo da Vinci (idraulica e cosmografia) della biblioteca di Lord Leicester in Holkham Hall, pubblicato sotto gli auspici del Reale Istituto Lombardo di Scienze e Lettere, Milan, Premio Tomasoni (Milan: L.F. Cogliati, 1909), and confirmed by Carlo Pedretti, The Codex Hammer of Leonardo da Vinci, translated into English and annotated by Carlo Pedretti (Florence: Giunti Barbèra, 1987), 182-83. See also Claire Farago, “The Codex Leicester,” in Leonardo da Vinci, Master Draftsman, edited by Carmen C. Bambach, exh. cat. (New York, NY, Metropolitan Museum of Art, 2003), 191-201; Christie, Manson & Woods International Inc., The Leonardo da Vinci Codex Hammer: the property of the Armand Hammer Museum of Art and Cultural Center, Los Angeles, California: Friday, November 11, 1994 (New York, N.Y.: Christie, Manson & Woods International Inc.), 28; Claire Farago, Martin Kemp, Owen Gingerich, Carlo Pedretti, eds., Codex Leicester: A Masterpiece of Science, exh. cat. (New York, NY: American Museum of Natural History, 1996), 32.
[31] Laurenza and Kemp 2019-2020, vol. 2, 15-16 and Domenico Laurenza, “The Compilation of the Codex Leicester: An Insight into Leonardo’s Research Style,” in Paolo Galluzzi and Alessandro Nova, eds., Decoding Leonardo’s Codices: Compilation, Dispersal, and Reproduction Technologies (Venice: Marsilio, 2019).
[32] Martin Kemp and Domenico Laurenza, “Compilation and Chaos,” vol. 2, 15-16. It should be noted that moldmate and twin sequences are disrupted by Laurenza’s proposed reordering.
[33] Bambach, Leonardo da Vinci Rediscovered, vol. 4, Appendix I, 1.
[34] The dimensions of the opened bi-folios are approximately 205 x 290 mm (8 3/32” x 11 14/32”); their edges have been trimmed. The quarto-sized Codex Arundel was made by folding in half a paper having a large rezzuta format, the same format as the sheets in the Codex Leicester. The folded paper is, in turn, folded in half again. In this arrangement, the sheet’s watermark is located in the center fold line of the manuscript, where it is less likely to be completely obscured by writing.
[35] See note 21.
[36] Pedretti and Vecce retain Arundel f. 18v (127) and Arundel ff. 16r-17v (123) as among the first 30 bi-folios and half sheets of the Codex Arundel (115-134); Pedretti and Vecce, Il Codice Arundel 263 nella British Library, vol. 4, 58.
[37] Margaret Holben Ellis and C. Richard Johnson, Jr., “Computational Connoisseurship: Enhanced Examination Using Automated Image Analysis,” Visual Resources Special Issue on Digital Art History 35, nos. 1-2 (March-June 2019): 125–140.
[38] Gorske, et al., International Journal for Digital Art History, March 2021.
[39] Most recently, Donnithorne, Leonardo da Vinci, 2019; Clayton, Leonardo da Vinci, 2018; Barone, ed., A Mind in Motion, 2019; Bambach, Leonardo da Vinci Rediscovered, 2019; Menu, ed., Leonardo da Vinci’s Technical Practice, 2014; Spadaccini, ed., Leonardo da Vinci e il suo lascito, 2019; Musée du Louvre, Léonard de Vinci: Dessins et manuscrits, 2003; Laurenza and Kemp, eds., Leonardo da Vinci’s Codex Leicester: A New Edition, 2019-2020.
[40] Carmen C. Bambach, “On the Role of Scientific Evidence in the Study of Leonardo’s Drawings,” in Leonardo da Vinci’s Technical Practice: Paintings, Drawings and Influence, edited by Michel Menu (Paris: Hermann, 2014), 236.
[41] See, for example, Elizabeth H. Bernick, “Drawing Connections – New Discoveries Regarding Cesare da Sesto’s Sketchbook,” Master Drawings 57, no. 2 (2019): 147-196.
Concordance between the current foliation of the Codex Leicester and the foliation found in the The Codex Hammer of Leonardo da Vinci, ed. C. Pedretti, Florence, 1987
| 1A = 36v, 1r | 10A = 27v, 10r |
| 1B = 1v, 36r | 10B = 10v, 27r |
| 2A = 35v, 2r | 11A = 26v, 11r |
| 2B = 2v, 35r | 11B = 11v, 26r |
| 3A = 34v, 3r | 12A = 25v, 12r |
| 3B = 3v, 34r | 12B = 12v, 25r |
| 4A = 33v, 4r | 13A = 24v, 13r |
| 4B = 4v, 33r | 13B = 13v, 24r |
| 5A = 32v, 5r | 14A = 23v, 14r |
| 5B = 5v, 32r | 14B = 14v, 23r |
| 6A = 31v, 6r | 15A = 22v, 15r |
| 6B = 6v, 31r | 15B = 15v, 22r |
| 7A = 30v, 7r | 16A = 21v, 16r |
| 7B = 7v, 30r | 16B = 16v, 21r |
| 8A = 29v, 8r | 17A = 20v, 17r |
| 8B = 8v, 29r | 17B = 17v, 20r |
| 9A = 28v, 9r | 18A = 19v, 18r |
| 9B = 9v, 28r | 18B = 18v, 19r |
Concordance between the current foliation of the Codex Leicester and the foliation found in the The Codex Hammer of Leonardo da Vinci, ed. C. Pedretti, Florence, 1987.
| 1r = 1A | 13r = 13A | 25r = 12B |
| 1v = 1B | 13v = 13B | 25v = 12A |
| 2r = 2A | 14r = 14A | 26r = 11B |
| 2v = 2B | 14v = 14B | 26v = 11A |
| 3r = 3A | 15r = 15A | 27r = 10B |
| 3v = 3B | 15v = 15B | 27v = 10A |
| 4r = 4A | 16r = 16A | 28r = 9B |
| 4v = 4B | 16v = 16B | 28v = 9A |
| 5r = 5A | 17r = 17A | 29r = 8B |
| 5v = 5B | 17v = 17B | 29v = 8A |
| 6r = 6A | 18r = 18A | 30r = 7B |
| 6v = 6B | 18v = 18B | 30v = 7A |
| 7r = 7A | 19r = 18B | 31r = 6B |
| 7v = 7B | 19v = 18A | 31v = 6A |
| 8r = 8A | 20r = 17B | 32r = 5B |
| 8v = 8B | 20v = 17A | 32v = 5A |
| 9r = 9A | 21r = 16B | 33r = 4B |
| 9v = 9B | 21v = 16A | 33v = 4A |
| 10r = 10A | 22r = 15B | 34r = 3B |
| 10v = 10B | 22v = 15A | 34v = 3A |
| 11r = 11A | 23r = 14B | 35r = 2B |
| 11v = 11B | 23v = 14A | 35v = 2A |
| 12r = 12A | 24r = 13B | 36r = 1B |
| 12v = 12B | 24v = 13A | 36v = 1A |
